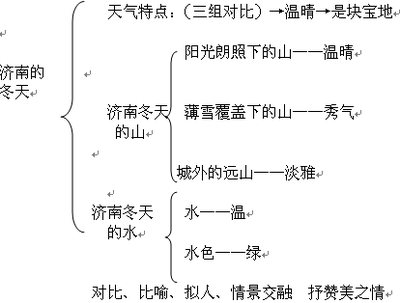
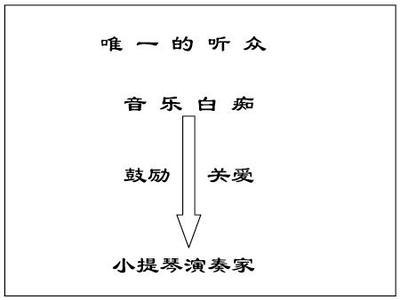
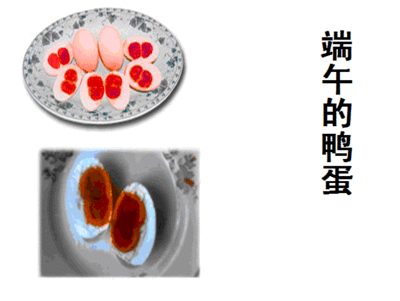
《平行线的判定》课堂实录
三宝中学 孟令梅
师:在上节课了我们学习了平行线、平行公理及其推论等知识。那么,老师现在就来考考大家,有谁知道平行线我们是如何定义的?
生1:不相交的两条直线是平行线。
师:她这样回答准确吗?
生2:在同一平面内,不相交的两条直线是平行线。
师:那么我们如果用平行线的定义来判断两条直线是否平行容易吗?
生3不容易,因为直线是无限伸长的,我们无法确定它们是否有交点。
师:那么我们有没有其他的方法来判定两条直线是否平行呢?今天我们就一起来探讨这个问题.(板书课题)
师:首先,我们先来看这样几个问题(多媒体展示)你能回答下面的问题吗?
(1)如图,直线a,b被直线c截,
其中同位角有——对,它们分别是————————;
内错角有——对,它们分别是————————;
同旁内角有——对,它别是————————————.
(2).填空:经过直线外一点,________与这条直线平行.
(3)思考:怎样过直线外一点画已知直线的平行线?
生:思考后回答
师:多媒体展示并评价学生的回答,尤其是在回答第3个问题时配合学生用多媒体演示做平行线的方法。
师问:在用三角尺画平行线过程中,三角尺起着什么样的作用?
生:根据同位角的意义以及平推三角尺画出平行线的过程,用自己的语言叙述判定两条直线平行的方法
师:引导学生正确表达平行线的判定方法1,并板书.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单记为:同位角相等,两条直线平行.
师:引导学生,结合图形用符号语言
表达两直线平行的判定方法1 : 如果∠1=∠2,那么AB∥CD. :
师强调:判定两直线平行方法1的条件中有两层意思:
①涉及到的两个角是两条直线被第三条直线所截而成的一对同位角;
A |
B |
C |
D |
1 |
3 |
4 |
5 |
2 |
E |
H |
F |
师:出示针对练习。
如果 ∠1=∠2, 能判定哪两条直线平行?
如果∠2=∠5呢,能判定哪两条直线平行?
如果∠3=∠4 呢,能判定哪两条直线平行?
G |
师:请同学们想一想,两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?(同时多媒体展示探究二)
探究二:已知∠2=∠3,直线AB与CD平行吗?
生:讨论交流,尝试写出说理过程
师生共同归纳判定方法二,
师:出示针对练习
如图,∠1= ∠2 ,且∠2=∠3,
AB和CD平行吗?
生:运用所学知识,独立解决问题
师:同旁内角数量上满足什么关系时,两直线平行?
生:通过观察,猜想,得出结论。
师:你能证明你的结论吗?(多媒体出示探究三)
生:合作探究
师:根据学生说理,再准确地板书:
因为∠4+∠2=180°,而∠4+∠1=180°,根据同角的补角相等,所以有∠2=∠1, 即同位角相等,从而a∥b.
因为∠4+∠2=180°,而∠4+∠3=180°,根据同角的补角相等,所以有∠3=∠2, 即内错角相等,从而a∥b.
师生共同归纳判定方法三(师板书)
师:出示针对练习
如图:ÐB= ÐD=45°,ÐC=135°,
生:合作交流,利用所学知识解决问题
师:我们现在已学习了几种方法来判定两条直线是否平行呢?它们分别为什么?
生2归纳,师展示表格,生6填空。
师:出示例题
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
生:小组探讨,交流找到不同方法后展示。
师:看来我们在解决问题时,方法是不唯一的,希望同学们发挥自己的聪明才智找到更好的方法。
师:下面我们就来应用我们所学的知识来解决几个问题(多媒体展示练习题)(略)
生:独立完成1-6题(略)
F |
D |
C |
A |
B |
E |
1 |
若不能判断AB∥DF,你认为还需要再添加的一个
2 |
生:合作交流讨论后小组代表展示讨论结果。
师:我们一定要明确三个判定方法的前提,
1必须是两条直线被第三条直线所截的形成的同位角,内错角,同旁内角。
2同位角,内错角,同旁内角必须满足特定条件。即同位角相等,或内错角相等,或同旁内角互补,两直线才能平行。
师:本节课你有什么收获呢?
生4:我学会了判定两条直线平行的三种方法
生5:是四种,在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
师:很好,同学们很善于总结。实际上我们这节课是通过具有特殊位置关系的角之间的数量关系,得到了两条直线之间的位置关系。这也体现了数学中的数形结合思想。
这节课我们就上到这里,今天的作业是课本17页第4、7题,谢谢同学们的配合,同学们再见!
《平行线的判定》课堂实录
三宝中学 孟令梅
师:在上节课了我们学习了平行线、平行公理及其推论等知识。那么,老师现在就来考考大家,有谁知道平行线我们是如何定义的?
生1:不相交的两条直线是平行线。
师:她这样回答准确吗?
生2:在同一平面内,不相交的两条直线是平行线。
师:那么我们如果用平行线的定义来判断两条直线是否平行容易吗?
生3不容易,因为直线是无限伸长的,我们无法确定它们是否有交点。
师:那么我们有没有其他的方法来判定两条直线是否平行呢?今天我们就一起来探讨这个问题.(板书课题)
师:首先,我们先来看这样几个问题(多媒体展示)你能回答下面的问题吗?
(1)如图,直线a,b被直线c截,
其中同位角有——对,它们分别是————————;
内错角有——对,它们分别是————————;
同旁内角有——对,它别是————————————.
(2).填空:经过直线外一点,________与这条直线平行.
(3)思考:怎样过直线外一点画已知直线的平行线?
生:思考后回答
师:多媒体展示并评价学生的回答,尤其是在回答第3个问题时配合学生用多媒体演示做平行线的方法。
师问:在用三角尺画平行线过程中,三角尺起着什么样的作用?
生:根据同位角的意义以及平推三角尺画出平行线的过程,用自己的语言叙述判定两条直线平行的方法
师:引导学生正确表达平行线的判定方法1,并板书.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单记为:同位角相等,两条直线平行.
师:引导学生,结合图形用符号语言
表达两直线平行的判定方法1 : 如果∠1=∠2,那么AB∥CD. :
师强调:判定两直线平行方法1的条件中有两层意思:
①涉及到的两个角是两条直线被第三条直线所截而成的一对同位角;
A |
B |
C |
D |
1 |
3 |
4 |
5 |
2 |
E |
H |
F |
师:出示针对练习。
如果 ∠1=∠2, 能判定哪两条直线平行?
如果∠2=∠5呢,能判定哪两条直线平行?
如果∠3=∠4 呢,能判定哪两条直线平行?
G |
师:请同学们想一想,两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?(同时多媒体展示探究二)
探究二:已知∠2=∠3,直线AB与CD平行吗?
生:讨论交流,尝试写出说理过程
师生共同归纳判定方法二,
师:出示针对练习
如图,∠1= ∠2 ,且∠2=∠3,
AB和CD平行吗?
生:运用所学知识,独立解决问题
师:同旁内角数量上满足什么关系时,两直线平行?
生:通过观察,猜想,得出结论。
师:你能证明你的结论吗?(多媒体出示探究三)
生:合作探究
师:根据学生说理,再准确地板书:
因为∠4+∠2=180°,而∠4+∠1=180°,根据同角的补角相等,所以有∠2=∠1, 即同位角相等,从而a∥b.
因为∠4+∠2=180°,而∠4+∠3=180°,根据同角的补角相等,所以有∠3=∠2, 即内错角相等,从而a∥b.
师生共同归纳判定方法三(师板书)
师:出示针对练习
如图:ÐB= ÐD=45°,ÐC=135°,
生:合作交流,利用所学知识解决问题
师:我们现在已学习了几种方法来判定两条直线是否平行呢?它们分别为什么?
生2归纳,师展示表格,生6填空。
师:出示例题
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
生:小组探讨,交流找到不同方法后展示。
师:看来我们在解决问题时,方法是不唯一的,希望同学们发挥自己的聪明才智找到更好的方法。
师:下面我们就来应用我们所学的知识来解决几个问题(多媒体展示练习题)(略)
生:独立完成1-6题(略)
F |
D |
C |
A |
B |
E |
1 |
若不能判断AB∥DF,你认为还需要再添加的一个
2 |
生:合作交流讨论后小组代表展示讨论结果。
师:我们一定要明确三个判定方法的前提,
1必须是两条直线被第三条直线所截的形成的同位角,内错角,同旁内角。
2同位角,内错角,同旁内角必须满足特定条件。即同位角相等,或内错角相等,或同旁内角互补,两直线才能平行。
师:本节课你有什么收获呢?
生4:我学会了判定两条直线平行的三种方法
生5:是四种,在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
师:很好,同学们很善于总结。实际上我们这节课是通过具有特殊位置关系的角之间的数量关系,得到了两条直线之间的位置关系。这也体现了数学中的数形结合思想。
这节课我们就上到这里,今天的作业是课本17页第4、7题,谢谢同学们的配合,同学们再见!
《平行线的判定》课堂实录
三宝中学 孟令梅
师:在上节课了我们学习了平行线、平行公理及其推论等知识。那么,老师现在就来考考大家,有谁知道平行线我们是如何定义的?
生1:不相交的两条直线是平行线。
师:她这样回答准确吗?
生2:在同一平面内,不相交的两条直线是平行线。
师:那么我们如果用平行线的定义来判断两条直线是否平行容易吗?
生3不容易,因为直线是无限伸长的,我们无法确定它们是否有交点。
师:那么我们有没有其他的方法来判定两条直线是否平行呢?今天我们就一起来探讨这个问题.(板书课题)
师:首先,我们先来看这样几个问题(多媒体展示)你能回答下面的问题吗?
(1)如图,直线a,b被直线c截,
其中同位角有——对,它们分别是————————;
内错角有——对,它们分别是————————;
同旁内角有——对,它别是————————————.
(2).填空:经过直线外一点,________与这条直线平行.
(3)思考:怎样过直线外一点画已知直线的平行线?
生:思考后回答
师:多媒体展示并评价学生的回答,尤其是在回答第3个问题时配合学生用多媒体演示做平行线的方法。
师问:在用三角尺画平行线过程中,三角尺起着什么样的作用?
生:根据同位角的意义以及平推三角尺画出平行线的过程,用自己的语言叙述判定两条直线平行的方法
师:引导学生正确表达平行线的判定方法1,并板书.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单记为:同位角相等,两条直线平行.
师:引导学生,结合图形用符号语言
表达两直线平行的判定方法1 : 如果∠1=∠2,那么AB∥CD. :
师强调:判定两直线平行方法1的条件中有两层意思:
①涉及到的两个角是两条直线被第三条直线所截而成的一对同位角;
A |
B |
C |
D |
1 |
3 |
4 |
5 |
2 |
E |
H |
F |
师:出示针对练习。
如果 ∠1=∠2, 能判定哪两条直线平行?
如果∠2=∠5呢,能判定哪两条直线平行?
如果∠3=∠4 呢,能判定哪两条直线平行?
G |
师:请同学们想一想,两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?(同时多媒体展示探究二)
探究二:已知∠2=∠3,直线AB与CD平行吗?
生:讨论交流,尝试写出说理过程

师生共同归纳判定方法二,
师:出示针对练习
如图,∠1= ∠2 ,且∠2=∠3,
AB和CD平行吗?
生:运用所学知识,独立解决问题
师:同旁内角数量上满足什么关系时,两直线平行?
生:通过观察,猜想,得出结论。
师:你能证明你的结论吗?(多媒体出示探究三)
生:合作探究
师:根据学生说理,再准确地板书:
因为∠4+∠2=180°,而∠4+∠1=180°,根据同角的补角相等,所以有∠2=∠1, 即同位角相等,从而a∥b.
因为∠4+∠2=180°,而∠4+∠3=180°,根据同角的补角相等,所以有∠3=∠2, 即内错角相等,从而a∥b.
师生共同归纳判定方法三(师板书)
师:出示针对练习
如图:ÐB= ÐD=45°,ÐC=135°,
生:合作交流,利用所学知识解决问题
师:我们现在已学习了几种方法来判定两条直线是否平行呢?它们分别为什么?
生2归纳,师展示表格,生6填空。
师:出示例题
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
生:小组探讨,交流找到不同方法后展示。
师:看来我们在解决问题时,方法是不唯一的,希望同学们发挥自己的聪明才智找到更好的方法。
师:下面我们就来应用我们所学的知识来解决几个问题(多媒体展示练习题)(略)
生:独立完成1-6题(略)
F |
D |
C |
A |
B |
E |
1 |
若不能判断AB∥DF,你认为还需要再添加的一个
2 |
生:合作交流讨论后小组代表展示讨论结果。
师:我们一定要明确三个判定方法的前提,
1必须是两条直线被第三条直线所截的形成的同位角,内错角,同旁内角。
2同位角,内错角,同旁内角必须满足特定条件。即同位角相等,或内错角相等,或同旁内角互补,两直线才能平行。
师:本节课你有什么收获呢?
生4:我学会了判定两条直线平行的三种方法
生5:是四种,在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
师:很好,同学们很善于总结。实际上我们这节课是通过具有特殊位置关系的角之间的数量关系,得到了两条直线之间的位置关系。这也体现了数学中的数形结合思想。
这节课我们就上到这里,今天的作业是课本17页第4、7题,谢谢同学们的配合,同学们再见!
 爱华网
爱华网